K-means Clustering

Tổng quan

1. Giới thiệu

1.1 Clustering

  • Phân cụm (Clustering) là một trong những kỹ thuật phân tích dữ liệu thăm dò phổ biến nhất được sử dụng để có được cái nhìn khách quan về dữ liệu.
  • Nhiệm vụ xác định các nhóm con trong dữ liệu sao cho các điểm dữ liệu trong các cụm (nhóm ) rất giống nhau trong khi các điểm dữ liệu trong các cụm khác nhau rất khác nhau. Nói cách khác, nó cố gắng tìm các nhóm con đồng nhất trong dữ liệu sao cho các điểm dữ liệu trong mỗi cụm giống nhau nhất có thể theo một thước đo như khoảng cách Euclidean hoặc khoảng cách dựa trên tương quan.
  • Tùy vào ứng dụng của mô hình mà lựa chọn sử dụng một độ đo hợp lý.
  • Các ứng dụng phổ biến của phân cụm:
    • Phân khúc thị trường.
    • Phân đoạn hoặc nén hình ảnh.
    • Phân nhóm tài liệu dựa trên các chủ đề.
  • Khác với học có giám sát, phân cụm được coi là phương pháp học không giám sát vì chúng ta không có dữ liệu mẫu để so sánh đầu ra của thuật toán phân cụm với các nhãn thực để đánh giá hiệu suất của nó.
  • Ta chỉ muốn cố gắng điều tra cấu trúc của dữ liệu bằng cách nhóm các điểm dữ liệu thành các nhóm nhỏ riêng biệt.

1.2 K-means

  • Là một trong những thuật toán học không giám sát (unsupervised learning) đơn giản và phổ biến nhất giải quyết vấn đề phân cụm.
  • Thông thường các thuật toán học không giám sát tạo ra các kết luận từ bộ dữ liệu đầu vào mà không đề cập đến kết quả đã biết hoặc đã được gán nhãn.
  • AndreyBu, một người có nhiều năm kinh nghiệm trong lĩnh vực học máy từng phát biểu rằng:

    The objective of K-means is simple: group similar data points together and discover underlying patterns. To achieve this objective, K-means looks for a fixed number $K$ of clusters in a dataset.

  • Một cụm đề cập đến một tập hợp các điểm dữ liệu được tổng hợp lại với nhau vì những điểm tương đồng nhất định.
  • Bạn sẽ phải xác định số mục tiêu $K$ , trong đó đề cập đến số lượng trọng tâm (centroids) bạn cần trong bộ dữ liệu. Một trọng tâm là vị trí tưởng tượng hoặc thực sự đại diện cho trọng tâm của cụm.
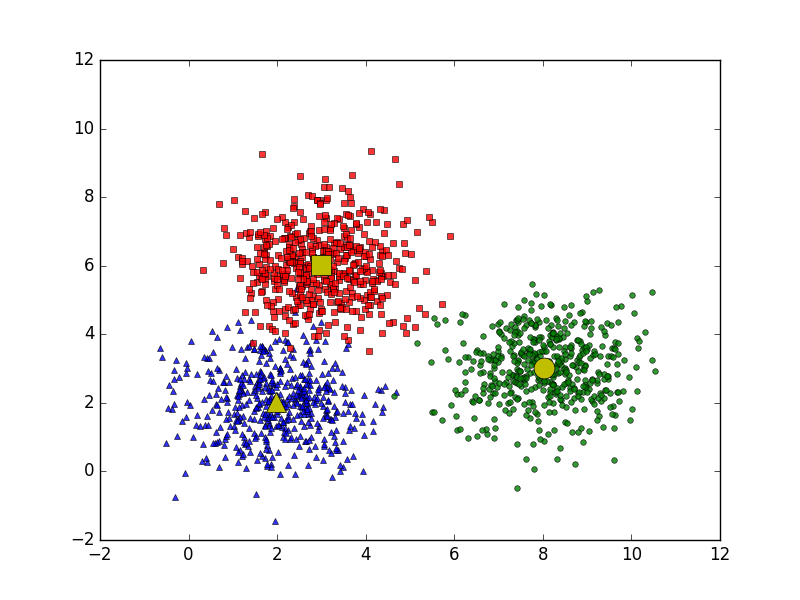Bài toán với 3 trọng tâm
  • Nói một cách đơn giản thì K-means xác định $K$ trọng tâm và phân bổ dữ liệu vào các cụm sao cho tổng khoảng cách giữa các điểm và trọng tâm của nó càng nhỏ càng tốt.
  • Ngắn gọn thì K-means là đi tìm trọng tâm để phân thành các cụm hoặc các nhóm (cluster).

2. Ý tưởng chính

Thuật toán phổ biến nhất dùng trong K-means là kỹ thuật lặp (iterative refinement technique), do nó khá phổ biến nên thường được gọi là thuật toán K-means.

2.1 Tóm tắt thuật toán

Dữ liệu đầu vào: dữ liệu $X$ và số lượng cụm $K$

Dữ liệu đầu ra: Các trọng tâm $M$ và vectơ phân cụm cho từng điểm dữ liệu $Y$

Các bước thực hiện:

  1. Chọn $K$ điểm bất kỳ làm các trọng tâm ban đầu.
  2. Phân mỗi điểm dữ liệu vào cụm có trọng tâm gần nó nhất
  3. Nếu việc gán dữ liệu vào từng cụm ở bước 2 không thay đổi so với vòng lặp trước nó thì ta dừng thuật toán.
  4. Cập nhật trọng tâm cho từng cụm bằng cách lấy trung bình cộng của tất các các điểm dữ liệu đã được gán vào cụm đó sau bước 2.
  5. Quay lại bước 2
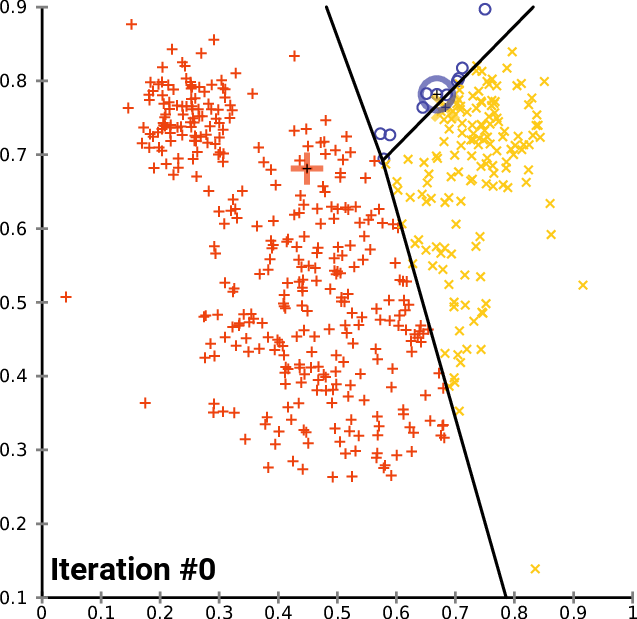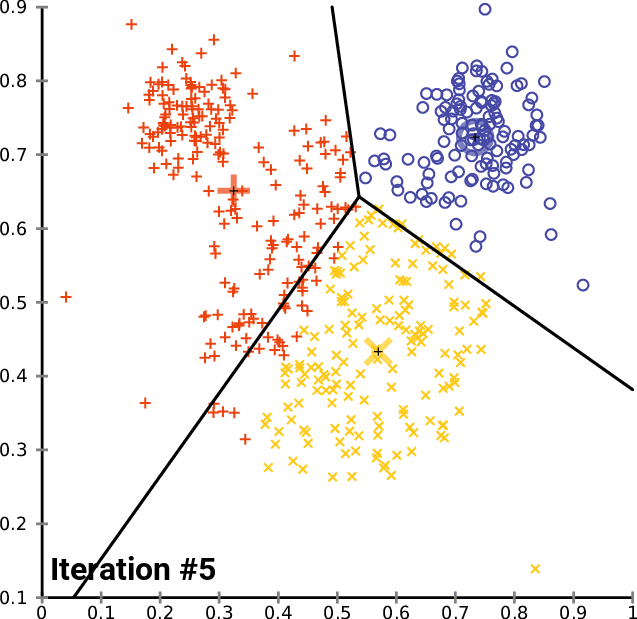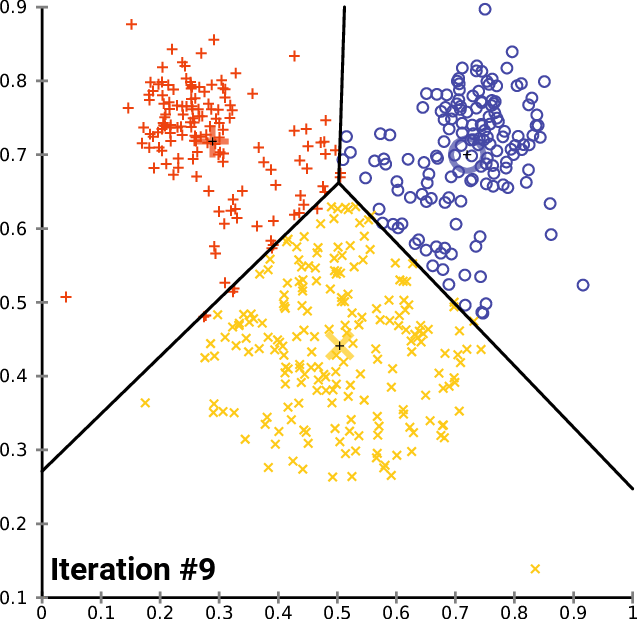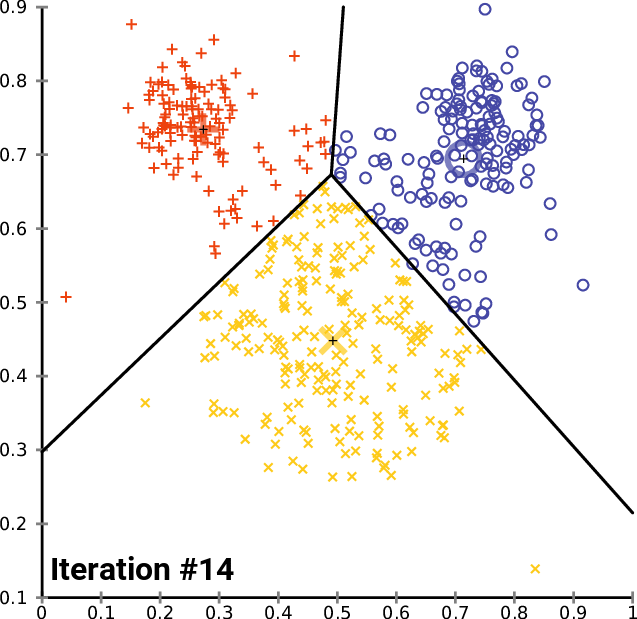Sự hội tụ của K-means

Nào! Ta cùng vào phần tiếp theo để hiểu rõ hơn cách thức hoạt động của thuật toán.

2.2 Hàm mất mát và phương pháp tối ưu

2.2.1 Hàm mất mát

Giả sử ta có $N$ điểm dữ liệu là $X=[x_1,x_2,...,x_N]$ và điều ta muốn là phân $N$ điểm dữ liệu đó thành $K$ cụm khác nhau. Điều chúng ta cần tìm là các trọng tâm $m_1, m_2,...,m_k$ của $K$ và gán nhãn từng điểm dữ liệu vào các cụm tương ứng.

Với mỗi điểm dữ liệu $x_i$ đặt $y_i=[y_{i1},y_{i2},...,y_{iK}]$ là vectơ nhãn, trong đó nếu $x_i$ thuộc vê cụm thứ $k$ thì $y_{ik}=1$ và $y_{ij}=0$ với $\forall i \neq k$. $\implies \begin{cases} y_{ik} \in \{0,1\}\\ \sum_{j=1}^Ky_{ij}=1 \end{cases} \quad (1)$

Ví dụ: nếu điểm dữ liệu có vectơ nhãn là $[1,0,0,...,0]$ thì nó sẽ thuộc vào cụm thứ 1

Cách mã hóa nhãn của dữ liệu thế này được gọi là biểu diễn one-hot (một cách biểu diễn khá phổ biến trong học máy)

Nếu ta coi $m_k$ là trọng tâm của cụm thứ $k$ thì tất cả các điểm dữ liệu $x_i$ được phân vào cụm $k$ sẽ có khoảng cách đến trọng tâm là $||x_i-m_k||_2^2$.

Điều ta muốn là khoảng cách này phải nhỏ nhất và vì $x_i$ được phân vào cụm $k$ nên $y_{ik}=1$ và $y_{ij}=0$ với $\forall i \neq k$. Khi đó khoảng cách của mỗi điểm đến trọng tâm của nó sẽ được viết lại như sau: $$y_{ik}||x_i-m_k||_2^2$$ Và ứng với $K$ cụm thì ta có tổng khoảng cách sẽ là: $$\sum_{j=1}^Ky_{ij}||x_i-m_j||^2_2$$ Từ đó thì ta suy ra khoảng cách của toàn bộ dữ liệu đến các trọng tâm là: $$L(Y,M)=\sum_{i=0}^N\sum_{j=1}^Ky_{ij}||x_i-m_j||^2_2$$ Trong đó $Y=[y_1,y_2,...,y_N]$ là ma trận tạo bởi các vectơ nhãn của từng điểm dữ liệu, $M=[m_1,m_2,...,m_k]$ là ma trận tạo bởi các trọng tâm của $K$ cụm cần phân chia.

Hàm số $L(Y,M)$ trên là hàm mất mát của thuật toán K-means thỏa điều kiện $(1)$.

Tóm lại điều ta cần là tối bài toán: $$Y,M=\arg \min_{Y,M}\sum_{i=0}^N\sum_{j=1}^Ky_{ij}||x_i-m_j||^2_2 \quad (2)$$

Với điều kiện: $\begin{cases} y_{ik} \in \{0,1\}\\ \sum_{j=1}^Ky_{ij}=1 \end{cases}$

2.2.1 Phương pháp tối ưu

Một cách đơn giản để tìm nghiệm tối ưu cho phương trình $(2)$ là ta sẽ thay phiên tìm $Y$ và $M$ trong khi cố định biến còn lại. Đây chính cũng chính là thuật toán K-means ta nêu ở trên.

Cố định $M$, giải tìm $Y$

Giả sử đã tìm được các trọng tâm, hãy tìm các vectơ nhãn để hàm mất mát đạt giá trị nhỏ nhất.

Điều này tương ứng với tìm cụm tương ứng cho mỗi điểm dữ liệu.

Khi các cụm cố định thì bài toán của ta được chia nhỏ ra thành tìm vectơ nhãn cho từng điểm dữ liệu $x_i$ như sau:$$y_i=\arg\min_{y_i}\sum_{i=1}^Ky_{ij}||x_i-m_j||_2^2 \quad (3)$$

Điều kiện: $\begin{cases} y_{ik} \in \{0,1\}\\ \sum_{j=1}^Ky_{ij}=1 \end{cases}$

Vì chỉ có một phần tử của vectơ nhãn $y_i$ bằng $1$ nên phương trình (3) được viết lại là: $$j=\arg\min_j||x_i-m_j||_2^2$$

Ta có $||x_i-m_j||_2^2$ chính là bình phương khoảng cách của $x_i$ đến $m_j$ vì vậy ta có thể thấy $x_i$ sẽ thuộc vào cụm có tâm gần nó nhất, từ đó suy ra vectơ nhãn của $x_i$.

Cố định $Y$, giải tìm $M$

Giả sử đã tìm được cụm cho từng điểm, hãy tìm trọng tâm mới cho mỗi cụm để hàm mất mát đạt giá trị nhỏ nhất.

Một khi chúng ta đã xác định được vectơ nhãn cho từng điểm dữ liệu, bài toán tìm trọng tâm cho mỗi cụm được rút gọn thành: $$l(m_j)=\arg \min_{m_j}\sum_{i=1}^Ny_{ij}||x_i-m_j||^2_2 \quad (3)$$ Ta có thể thấy phương trình $(3)$ là một hàm liên tục và có đạo hàm tại mọi điểm nên ta có thể tìm nghiệm bằng cách giải phương trình đạo hàm bằng $0$ .

Lấy đạo hàm theo biến $m_j$ ta có: $$\frac{\partial l(m_j)}{\partial m_j}=2\sum_{i=1}^Ny_{ij}(m_j-x_i)$$

Giải phương trình đạo hàm bằng $0$ ta có: $$m_j=\frac{\sum_{i=1}^Ny_{ij}x_j}{\sum_{i=1}^Ny_{ij}}$$ Như ta thấy thì nghiệm là trung bình của các phần tử thuộc mỗi cụm $j$. Cái tên K-means cũng xuất phát từ đây.

3. Demo đơn giản

Chúng ta cùng xem một demo nhỏ để thấy thuật toán hoạt động như thế nào trên dữ liệu nhé.

Trước tiên ta sẽ sinh ngẫu nhiên một bộ dữ liệu với 3 cụm, 150 điểm dữ liệu với độ lệch chuẩn là $0.5$

In [9]:
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
                    n_features=2,
                    centers=3,
                    cluster_std=0.5,
                    shuffle=True,
                    random_state=0)
import matplotlib.pyplot as plt
plt.scatter(X[:, 0],
X[:, 1],
c='white',
marker='o',
edgecolor='black',
s=50)
plt.grid()
plt.tight_layout()
plt.show()

Dữ liệu sẽ được như hình bên trên. Sau đó ta sẽ sử dụng mô hình K-means của thư viện sklearn để thực hiện phân cụm dữ liệu bên trên.

In [2]:
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
             init='random',
             n_init=10,
             max_iter=300,
             tol=1e-04,
             random_state=0)
y_km = km.fit_predict(X)

Dưới đây là hình vẽ sau khi phân thành 3 cụm

In [3]:
plt.scatter(X[y_km == 0, 0],
            X[y_km == 0, 1],
            s=50, c='lightgreen',
            marker='s', edgecolor='black',
            label='Cluster 1')
plt.scatter(X[y_km == 1, 0],
            X[y_km == 1, 1],
            s=50, c='orange',
            marker='o', edgecolor='black',
            label='Cluster 2')
plt.scatter(X[y_km == 2, 0],
            X[y_km == 2, 1],
            s=50, c='lightblue',
            marker='v', edgecolor='black',
            label='Cluster 3')
plt.scatter(km.cluster_centers_[:, 0],
            km.cluster_centers_[:, 1],
            s=250, marker='*',
            c='red', edgecolor='black',
            label='Centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()

Như ta thấy thì thuật toán đã phân được thành 3 cụm rõ ràng cùng tìm được 3 trọng tâm ứng với mỗi cụm.

Các bạn có thể xem thuật thuật toán cập nhật các trọng tâm của mỗi cụm dữ liệu qua các trang sau:

Blog naftaliharris

Stanford

4. Kết luận

4.1 Ưu điểm

  • Đơn giản, dễ hiểu, tương đối hiệu quả.
  • Các đối tượng tự động gán vào nhóm.
  • Thường được tối ưu cục bộ.

4.2 Nhược điểm

  • Các thuộc tính không phải số.
  • Cần xác định số nhóm ($K$) trước.
  • Phụ thuộc vào việc chọn các nhóm đầu tiên.
  • Gặp vấn đề khi các nhóm có kích thước, mật độ khác nhau hoặc hình dáng không phải hình cầu.
  • Nhạy cảm với dữ liệu nhiễu.
  • Với những cụm dữ liệu chồng lên nhau thì sẽ phân loại sai.
    • Giả sử ta biết trước có 3 cụm dữ liệu như hình dưới
In [4]:
from __future__ import print_function 
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist
np.random.seed(11)
means = [[2, 2], [8, 3], [7, 2]]
cov = [[1, 0], [0, 1]]
N = 500
X0 = np.random.multivariate_normal(means[0], cov, N)
X1 = np.random.multivariate_normal(means[1], cov, N)
X2 = np.random.multivariate_normal(means[2], cov, N)
X = np.concatenate((X0, X1, X2), axis = 0)
K = 3
original_label = np.asarray([0]*N + [1]*N + [2]*N).T
In [5]:
def kmeans_display(X, label):
    K = np.amax(label) + 1
    X0 = X[label == 0, :]
    X1 = X[label == 1, :]
    X2 = X[label == 2, :]
    
    plt.plot(X0[:, 0], X0[:, 1], 's', markersize = 4, alpha = .8)
    plt.plot(X1[:, 0], X1[:, 1], 'o', markersize = 4, alpha = .8)
    plt.plot(X2[:, 0], X2[:, 1], 'v', markersize = 4, alpha = .8)

    plt.axis('equal')
    plt.plot()
    plt.show()
In [6]:
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
             init='random',
             n_init=10,
             max_iter=300,
             tol=1e-04,
             random_state=0)
y_km = km.fit_predict(X)
In [7]:
kmeans_display(X, original_label)
In [8]:
plt.scatter(X[y_km == 0, 0],
            X[y_km == 0, 1],
            s=50, c='lightgreen',
            marker='s', edgecolor='black',
            label='Cluster 1')
plt.scatter(X[y_km == 1, 0],
            X[y_km == 1, 1],
            s=50, c='orange',
            marker='o', edgecolor='black',
            label='Cluster 2')
plt.scatter(X[y_km == 2, 0],
            X[y_km == 2, 1],
            s=50, c='lightblue',
            marker='v', edgecolor='black',
            label='Cluster 3')
plt.scatter(km.cluster_centers_[:, 0],
            km.cluster_centers_[:, 1],
            s=250, marker='*',
            c='red', edgecolor='black',
            label='Centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()

- Như ta thấy thì khi dùng K-means để phân loại dữ liệu của ta thì tuy nó phân loại ra 3 cụm nhưng nó sai so với dữ liệu gốc. Điều này làm cho K-means ít được ứng dụng trong thực tế.

4.3 Ứng dụng

Thuật toán K-means được ứng dụng rất nhiều trong thực tế ở các lĩnh vực khác nhau.

  • Xử lý ảnh: Phân nhóm các chữ số viết tay, tách vật thể (image segmentation ), nén ảnh/dữ liệu ( image compression ),...
  • Các lĩnh vực khác như: phân cụm tài liệu, xác định các khu vực dễ phạm tội, phân khúc khách hàng, phát hiện gian lận bảo hiểm, phân tích dữ liệu giao thông công cộng, phân cụm cảnh báo CNTT,...

5. Tài liệu tham khảo

$^{[1]}$ Blog Machine Learning Cơ Bản - Vũ Hữu Tiệp - K-means

$^{[2]}$ Blog Naftaliharris: Visualizing K-Means Clustering

$^{[3]}$ Stanford-Visualizing K-Means Clustering

$^{[4]}$ Medium - Muhammad Rizwan Khan - K Means Clustering Algorithm & its Application

$^{[5]}$ Towardsdatascience - Imad Dabbura - K-means Clustering: Algorithm, Applications, Evaluation Methods, and Drawbacks

$^{[6]}$ k-means clustering algorithm

$^{[7]}$Towardsdatascience - Dr. Michael J. Garbade - Understanding K-means Clustering in Machine Learning

$^{[8]}$Geeksforgeeks - K means Clustering – Introduction

In [ ]: