Apriori Algorithm ¶
1. Giới thiệu¶
Khi chúng ta đi mua sắm, ta thường thấy những sản phẩm có liên quan đến nhau thường được đặt cạnh nhau để gợi cho người mua có thể sẽ mua sản phẩm đó. Tại sao họ biết mà sắp xếp được như vậy? Đó là dựa vào khai phá luật kết hợp.

Khai phá luật kết hợp là gì?¶

- Khai phá luật kết hợp (Association Rule Mining) được ứng dụng phổ biến trong kinh doanh. Nó được sử dụng rộng rãi để hiểu và thử nghiệm các chiến lược kinh doanh, tiếp thị khác nhau để tăng doanh số và năng suất của các tổ chức, bao gồm chuỗi siêu thị và thị trường trực tuyến.
- Khai phá luật kết hợp là học tập dựa trên quy tắc (rule-based learning) để xác định sự liên kết giữa các sản phẩm khác nhau trong cơ sở dữ liệu. Một trong những ví dụ tốt nhất và phổ biến nhất của Khai phá luật kết hợp là phân tích giỏ thị trường (Market Basket Analysis). Phân tích sự liên kết giữa các mặt hàng khác nhau có xác suất cao nhất được mua bởi khách hàng.
- Ví dụ, hiểu được thói quen mua hàng của khách hàng bằng cách tìm ra mối tương quan và mối liên hệ giữa các mặt hàng khác nhau mà khách hàng đặt trong ‘giỏ hàng của họ', từ đó có thể rút ra các mẫu theo định kỳ.
- Cụ thể, anh Dii đi mua một chai rượu trong siêu thị. Anh cũng lấy một vài gói khô bò. Người quản lý ở đó phân tích rằng, không chỉ anh Dii, mọi người thường có xu hướng mua rượu và khô bò cùng nhau. Sau khi tìm ra mô hình, người quản lý bắt đầu sắp xếp các mặt hàng này lại với nhau và sau đó đã có thông báo tăng doanh số.
- Quá trình xác định mối liên kết giữa các sản phẩm / mặt hàng được gọi là khai phá luật kết hợp. Để thực hiện khai thác quy tắc kết hợp, nhiều thuật toán đã được phát triển. Thuật toán Apriori là một trong những thuật toán phổ biến nhất và được cho là hiệu quả nhất trong số đó. Chúng ta tiếp tục thảo luận về thuật toán Apriori là gì nhé!
2. Thuật toán Apriori¶
2.1 Thuật toán Apriori là gì?¶
- Thuật toán được đề xuất lần đầu tiên vào năm 1994 bởi Rakesh Agrawal và Ramakrishnan Srikant, nó thực hiện việc tìm các mục hoặc phần tử thường xuyên nhất trong cơ sở dữ liệu giao dịch và xác định các quy tắc kết hợp giữa các mục giống như ví dụ đã đề cập ở trên.
- Theo thuật toán, bất kỳ tập hợp con của một tập hợp phổ biến thì phổ biến.
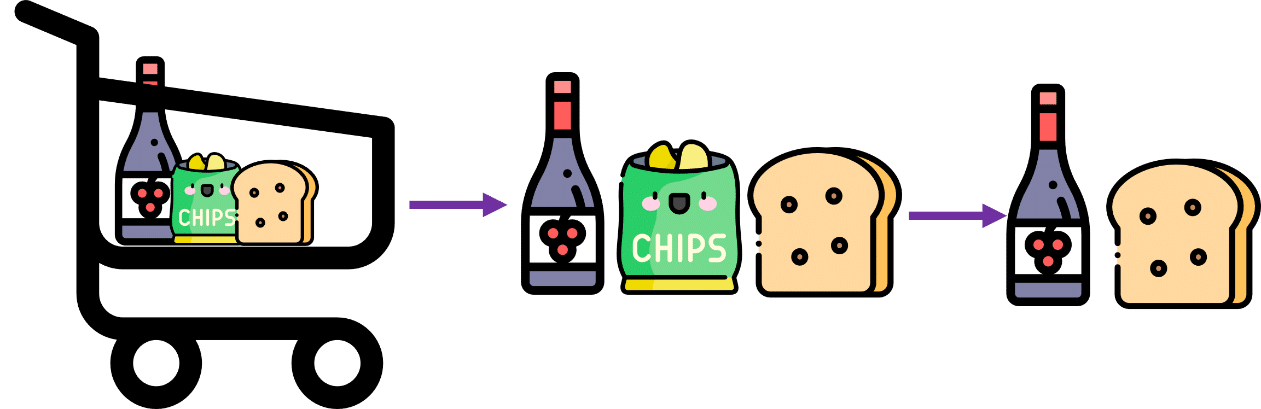
- Cụ thể, ta có 2 giao dịch (transaction) chứa {rượu vang, khoai tây chiên, bánh mì} và {rượu vang, bánh mì}. Vì vậy, theo nguyên tắc của Apriori, nếu {rượu, khoai tây chiên, bánh mì} là phổ biến, thì {rượu, bánh mì} cũng phải phổ biến.
2.2 Cách mà thuật toán Apriori làm việc?¶
- Ý tưởng chính trong thuật toán Apriori là tất cả các tập hợp con của một tập hợp mục (item) phổ biến là phổ biến. Tương tự, đối với bất kỳ mục (item) không phổ biến nào, tất cả các tập hợp con của nó cũng phải không phổ biến.
- Để hiểu hơn về thuật toán Apriori, ta sẽ đi qua một ví dụ: Ở đây , dataset chứa 6 giao dịch (transaction) trong một giờ, mỗi giao dịch thể hiện những sản phẩm được mua, 0 là không mua, 1 là mua.
- Dựa vào dataset trên, ta có thể tìm thấy các luật. Ví dụ như nếu Wine và Chips được mua, thì khách hàng cũng sẽ mua Bread
- Để tìm ra điều đó, ta phải sử dụng các độ đo sau:
- Support
- Confidence
- Lift
- Support: là tỉ lệ của số lượng các giao dịch có chứa tập các mặt hàng $A$ và tổng tất cả các giao dịch.
ex:
$Supp(wine) = \frac{4}{6} = 0.6667$
- Confidence: biểu thị khả năng tập các mặt hàng $B$ được mua khi $A$ được mua
ex:
$Conf(\text{{wine, chips}=> {bread}}) = \frac{\text{supp({wine, chips, bread})}}{\text{supp({wine, chips})}} = \frac{\frac{2}{6}}{\frac{3}{6}} = 0.667$
- Lift: biểu thị khả năng $B$ được mua khi $A$ được bán, thể hiện mức độ phổ biến $B$
ex:
$Lift(\text{{wine, chips}=> {bread}}) = \frac{\text{supp({wine, chips, bread})}}{\text{supp({wine, chips})*supp({bread})}} = \frac{\frac{2}{6}}{\frac{3}{6}*\frac{4}{6}} = 1$
Ta có:
- $Lift(A=>B) = 1$ nghĩa là không có mối tương quan trong các mục.
- $Lift(A=>B) > 1$ nghĩa là có một mối tương quan tích cực trong itemset, tức là $A$ và $B$ có nhiều khả năng được mua cùng nhau.
- $Lift(A=>B) < 1$ nghĩa là có một mối tương quan tiêu cực trong itemset, tức là $A$ và $B$ không có khả năng được mua cùng nhau.
3. Demo đơn giản¶
In [16]:
# Importing the required dataset
import numpy as np
import pandas as pd
from apyori import apriori
In [17]:
# Loading dataset
store_data = pd.read_csv('https://raw.githubusercontent.com/HuynhHoa99/AprioriAlgorithm/master/Day1.csv', header=None)
In [18]:
store_data.head()
Out[18]:
In [19]:
store_data.shape
Out[19]:
In [12]:
records = []
for i in range(22):
records.append([str(store_data.values[i, j]) for j in range(6)])
In [13]:
records
Out[13]:
In [14]:
association_rules = apriori(records, min_support=0.5, min_confidence=0.7, min_lift=1.2, min_length=2)
association_results = list(association_rules)
In [15]:
print(association_results)
- Giải thích kết quả:
- Giá trị hổ trợ (support) của luật đầu tiên là 0.5 (được tính bằng số lượng giao dịch chứa { ‘Milk,’ ‘Bread,’,‘Butter’} chia cho tổng số giao dịch).
- Mức độ tin cậy (confidence) cho luật là 0.846 (điều này cho thấy rằng trong số tất cả các giao dịch có chứa cả {'Milk', 'Bread'} thì có 84,6% cũng chứa ‘Butter').
- Mức độ tương quan (lift) là 1.241 cho chúng ta biết rằng ‘Butter’ có khả năng được mua nhiều hơn gấp 1,241 lần bởi những khách hàng mua cả ‘Milk’ và ‘Butter’ so với những người chỉ mua ‘Butter’.
4. Kết luận¶
4.1 Ứng dụng¶
- Việc thuật toán Apriori có thể làm là nhìn vào quá khứ và khẳng định rằng nếu một việc gì đó xảy ra thì sẽ có tỉ lệ bao nhiêu phần trăm sự việc tiếp theo sẽ xảy ra. Nó giống như nhìn vào quá khứ để dự đoán tương lại vậy, và việc này rất có ít cho các nhà kinh doanh.
4.2 Ưu điểm¶
- Đây là thuật toán đơn giản và dễ hiểu nhất trong số các thuật toán học quy tắc kết hợp.
- Các quy tắc kết quả là trực quan và dễ dàng để giao tiếp với người dùng cuối.
- Nó không yêu cầu dữ liệu được dán nhãn vì nó là thuật toán không giám sát, do đó bạn có thể sử dụng nó trong nhiều tình huống khác nhau vì dữ liệu không được gắn nhãn thường dễ truy cập hơn.
- Nhiều tiện ích mở rộng đã được đề xuất cho các trường hợp sử dụng khác nhau dựa trên triển khai này, ví dụ, có các thuật toán học liên kết có tính đến việc đặt hàng các mặt hàng, số lượng của chúng và khoảng thời gian liên quan.
4.3 Nhược điểm¶
- Phải duyệt CSDL nhiều lần. Với $I = {i_1, i_2, ..., i_{100}}$, số lần duyệt CSDL sẽ là 100.
- Số lượng tập ứng viên rất lớn: $2^{100} - 1 = 1.27 * 10^{30}$.
- Thực hiện việc tính độ phổ biến nhiều, đơn điệu.
4.4 Ý tưởng cải tiến¶
- Giảm số lần duyệt CSDL.
- Giảm số lượng tập ứng viên.
- Qui trình tính độ phổ biến thuận tiện hơn.
