K-Nearest Neighbors

1. Giới thiệu

K-Nearest Neighbors (KNN) là một thuật toán đơn giản, dùng cho cả bài toán phân loại (classifications) và hồi quy (regression). Khác với đa số thuật toán học máy khác, KNN không học từ dữ liệu mà mọi quá trình tính toán đều được thực hiện khi cần dự đoán kết quả của một điểm dữ liệu mới. Đây được xem như là một sự đánh đổi, khi không tốn chi phí training nhưng chi phí tính toán và bộ nhớ đòi hỏi lớn. Nó tốn chi phí bộ nhớ vì phải lưu trữ toàn bộ dữ liệu để phục vụ tính toán. Tương tự với chi phí tính toán, việc tìm ra kết quả của một điểm dữ liệu nhất định cần duyệt qua toàn bộ dữ liệu.

KNN là một phương pháp không tham số (non-parametric): số lượng tham số cố định không phụ thuộc vào kích cỡ cũng như số chiều của dữ liệu đầu vào. Đối với KNN, không phụ thuộc vào số lượng đặc trưng của dữ liệu, mô hình chỉ có duy nhất một tham số là $K$ (Hyperparameter - tham số được cho trước). Nó cũng không yêu cầu bất cứ giả định nào về phân phối dữ liệu như các thuật toán khác. Điều này mang lại cho KNN một lợi thế vượt trội trong các mô hình có dữ liệu phân phối không theo quy chuẩn nhất định (không tuyến tính). Đây là lý do để KNN là lựa chọn đầu tiên khi không có thông tin về phân phối dữ liệu.

2. Ý tưởng chính

KNN hoạt động dựa trên nguyên lý:

Gần mực thì đen, gần đèn thì sáng.

      Tục ngữ Việt Nam

Nghĩa là, khi bạn có các đặc trưng gần với một nhóm $K$ người nào đó thì KNN cho rằng bạn giống với số đông trong $K$ người đó. Nói cách khác, KNN dựa trên sự tương đồng giữa các đặc trưng để phân loại một điểm dữ liệu nhất định.

2.1 $K$ trong KNN

$K$ chỉ định số lượng điểm lân cận được xem xét đến khi quyết định kết quả của một điểm cần dự đoán. Đây là một tham số cực kì quan trọng khi làm việc với KNN. Nếu $K$ quá nhỏ, có thể dẫn đến độ tin cậy của mô hình không chính xác, nếu $K$ quá lớn sẽ dẫn đến tốn chi phí tính toán. Không có một giá trị $K$ nào được coi là tối ưu cho mọi bài toán sử dụng KNN, việc chọn giá trị của $K$ phụ thuộc vào từng trường hợp cụ thể và đôi khi phương pháp tốt nhất để chọn $K$ là chạy qua các giá trị khác nhau của $K$ và so sánh kết quả để tìm ra được giá trị $K$ tối ưu cho bài toán.

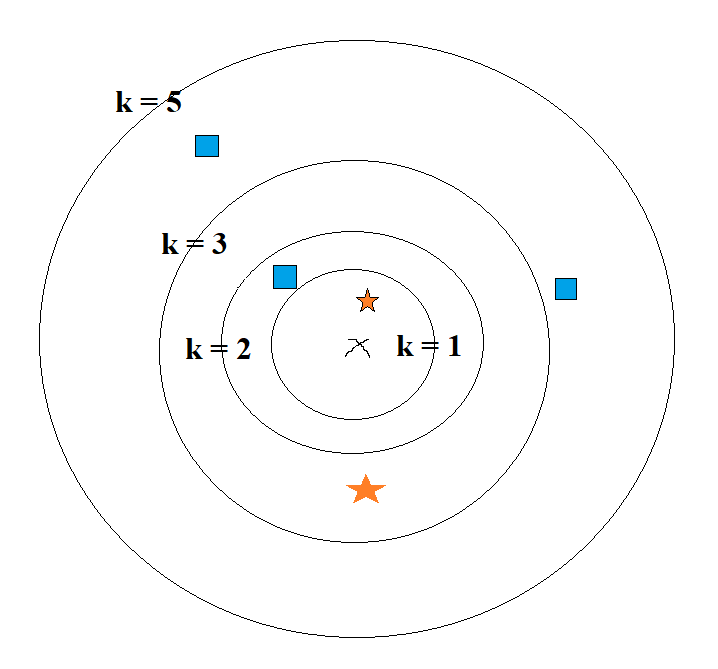
Minh hoạ tham số K
Minh hoạ tham số K

Với hình trên, khi:

  • $K$ = 1, x có giá trị là hình ngôi sao vì x gần nhất với ngôi sao trong vòng tròn $K$ = 1.
  • $K$ = 3, x có giá trị là ngôi sao vì trong vòng tròn $K$ = 3, có 2 ngôi sao và 1 hình vuông.
  • $K$ = 5, x có giá trị là hình vuông vì trong vòng trong $K$ = 5, có 2 ngôi sao và 3 hình vuông.
  • $K$ = 2, ta không xác định được giá trị của x vì số ngôi sao và hình vuông bằng nhau. Do đó ta nên tránh sử dụng $K$ là số chẵn.

2.2 Các độ đo khoảng cách

Tương tự như tham số $K$, KNN sử dụng nhiều độ đo khoảng cách khác nhau. Và không ai trong chúng ta có thể đảm bảo rằng một độ đo tốt hơn phần còn lại với mọi người hợp. Ý tưởng chính của việc chọn độ đo là: đâu là định nghĩa thích hợp nhất về độ đo cho dữ liệu hiện tại. Như vậy, ở phần này chúng ta sẽ điểm qua một số độ đo khoảng cách nổi bật:

2.2.1 Khoảng cách Euclidean

Đây là một trong số các độ đo được sử dụng phổ biến trong các mô hình học máy. Công thức của khoảng cách Euclidean như sau:

$$D(a, b) = \sqrt{\sum_i^n{(b_i - a_i)^2}}$$

2.2.2 Khoảng cách Hamming

Đây là độ đo được sử dụng khi làm việc với dữ liệu rời rạc (categorical data). Với một điểm dữ liệu nhất định, ta xét từng đặc trưng của điểm dữ liệu, nếu giá trị của nó giống với đặc trưng tương ứng của điểm dữ liệu mà khoảng cách đang được đo thì khoảng cách là 0, ngược lại khoảng cách là 1. Khoảng cách giữa 2 điểm dữ liệu sẽ bằng tổng khoảng cách giữa các đặc trưng của 2 điểm dữ liệu. Công thức cho khoảng cách Hamming là: $$D(a, b) = \sum_{i = 1}^n{(a_i \ne b_i)}$$ Trong đó:

  • $n$ là số lượng đặc trưng của dữ liệu.
  • $a_i$ là đặc trưng thứ $i$ của dữ liệu.

2.2.3 Khoảng cách Minkowski

Khoảng cách Euclide có thể được khái quát bằng cách sử dụng chuẩn Minkowski còn được gọi là chuẩn p. Công thức cho khoảng cách Minkowski là: $$D(a, b) = \sqrt[p]{|a_f -b_f|^p}$$ Trong đó:

  • $f$ là đặc trưng.
  • Tham số $p$ cho ta một lợi thế khi sử dụng khoảng cách Minkowski đó là có thể thay đổi giá trị của $p$ để có được các loại độ đo khoảng cách khác nhau.

2.2.4 Độ đo tự định nghĩa

Ngoài những độ đo nêu trên thì còn rất nhiều độ đo khác được phát triển bởi nhiều nhà nghiên cứu khác. Tuy nhiên, với KNN ta hoàn toán có thể tự định nghĩa độ đo mới cho phù hợp với thực tế bài toán, miễn là nó hợp lý và cho hiệu quả tốt.

3. Demo đơn giản

In [0]:
from mnist import MNIST
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
In [0]:
# Chuẩn bị dữ liệu
<<<<<<< HEAD
mndata = MNIST('mnist') # Tải dữ liệu tại http://yann.lecun.com/exdb/mnist/
=======
data = MNIST('mnist') # Tải dữ liệu tại http://yann.lecun.com/exdb/mnist/
>>>>>>> 0aa7c1572bec712bf8733c87dbd9adf9048705a8
data.load_testing()
data.load_training()
X_test = data.test_images
X_train = data.train_images
y_test = np.asarray(data.test_labels)
y_train = np.asarray(data.train_labels)
In [4]:
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X_train, y_train)
Out[4]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=3, p=2,
                     weights='uniform')
In [5]:
neigh.score(X_test[:1000], y_test[:1000])
Out[5]:
0.962

4. Kết luận

4.1 Ưu điểm

  • Không có giả định về phân bố dữ liệu.
  • Thuật toán đơn giản, dễ giải thích.
  • Có thể dùng cho cả phân loại và hồi quy.

4.2 Nhược điểm

  • Chi phí tính toán cao.
  • Yêu cầu bộ nhớ lớn.
  • Thời gian dự đoán có thể chậm O(n).

5. Tài liệu tham khảo

$^{[1]}$ Blog: Usejournal: A Quick Introduction to K-Nearest Neighbors Algorithm

$^{[2]}$ Datavedas: KNN - DISTANCE METRICS

$^{[3]}$ Wikipedia: K-nearest_neighbors_algorithm

$^{[4]}$ Springboard: KNN Machine Learning Algorithm Explained

$^{[5]}$ Machine learning cơ bản: K-nearest neighbors